Recall the following trigonometric identity
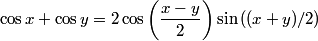 Let  and let and let 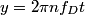 . Here, . Here, 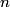 corresponds to the harmonic, corresponds to the harmonic, 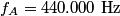 and and 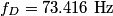 . .Then, the superposition of the two notes is 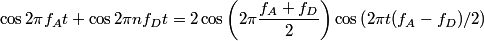 So, the beat frequency is 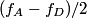 . The following table shows the value of . The following table shows the value of 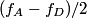 for various values of for various values of 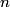 . . \begin{center}\begin{tabular}{|c|c|} \hline n & 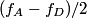 (in Hz)\\ (in Hz)\\\hline 1 & 183.292 \\ \hline 2 & 146.584 \\ \hline 3 & 109.876 \\ \hline 4 & 73.168 \\ \hline 5 & 36.46 \\ \hline 6 & 0.248 \\ \hline 7 & 36.956 \\ \hline \end{tabular}\end{center} So, clearly the smallest number of beats occurs when 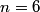 . Recall that a beat occurs whenever the second cosine factor equals . Recall that a beat occurs whenever the second cosine factor equals 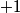 or or 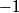 , therefore, the number of beats per second is , therefore, the number of beats per second is 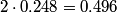 . Therefore, answer (B) is correct. . Therefore, answer (B) is correct. |